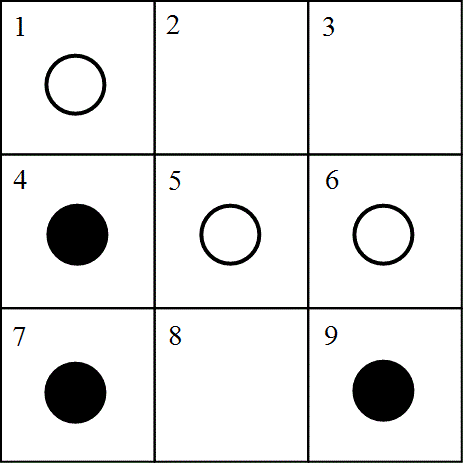
Let's just say that we are playing tic-tac-toe in a different manner. You all must be quite familiar with the game. Only, we have changed the rules slightly. Refer the picture. There are white and black markers instead of the usual circle and cross. They just represent two different people. Each player gets to play just three times. After that, he can only move the markers from one square to the adjacent empty square.
For example, if you see the figure, you will find that now, if it's white's turn, he can move from 6 to 3. And then whatever the black player may do, the next move that white will play will be moving the marker from 5 to 2 and he will win the game (three in a row).
Now, you have to acknowledge everything and decide that if both the players are playing with the perfect strategy, will the white player (the first to play) be the winner always? Or the black can win? Or they can lead the game to a draw every time?
Solution:
The best way to analyze the situation would be forcing a win for white when the black player plays anywhere but a corner square. Refer to the given figure for the current positions. Now, if black plays 7 to block the white player from having three in a row, white will move 5 to 6 and will win. But since you get to place only three markers, black can place the marker at 6 and white won't be able to add one more at 7 to win. And moving the 9 marker to 7 will take two steps.
But white can still get to square 7 before black is able to block him or form a three in a row. In this manner, no matter what black does, the white player can always win the game if he begins from the center square.






 Submit your Email Address to get latest post directly to your inbox.
Submit your Email Address to get latest post directly to your inbox.